Improving Elastic Search Query Result with Query Expansion using Topic Modeling
Query expansion is a process of reformulating a query to improve query results and to be more specific to improve the recall for a query. Topic modeling is an Natural Language Processing (NLP) technique to discover hidden topics or concepts in documents. We will be going through a Query Expansion technique based on Topic Modeling.
The solution is based on Latent Dirichlet Allocation (LDA) algorithm as implemented python gensim library. LDA is a popular Topic Modeling algorithm. The implementation is available from my open source project avenir in github. It provides an user friendly wrapper class around gensim LDA implementation.
Query Expansion
Query expansion is the technique of expanding the original query key words by adding additional words. It enables search engines to return content that may not contain the search key words. Query expansion increases recall, which is the fraction of relevant document that is retrieved. Increasing recall is often accompanied by decreasing precision, which is the fraction retrieved documents that are relevant. Essentially, false negatives go down while false positives go up, with query expansion.
Behind a set of search keywords, there is an intent on the part of the user. Query expansion is most effective, when the expanded query aligns with the intent the user has.There are many techniques for Query Expansion. Broadly, they fall into the following 2 categories
- Based on query vector only, also called global methods.
- Based on query vector and relevant documents, also called local methods
One simple example of the first approach is synonym of query words. One algorithm called Rochio algorithm is based on the second approach. It moves the original query vector towards the centroid of the relevant documents and away from the relevant documents.
Ideally, relevant documents should be based on documents, the user has interacted with based on the the results from the initial user query. In the absence of user interaction, we could take the top n documents from the initial query as relevant documents and the rest as irrelevant documents.
Topic Modeling
Vector representation of documents is typically based on a Bag of Words (BOW). With topic modeling, a document with BOW representation is transformed to a lower dimensional space in terms of topics or concepts.
For example, with some algorithms, a document is represented as a probability distribution over topics. The probability values could be considered to be the coordinates in the lower dimensional space.
As an example, when we read an article about word cup soccer final between Croatia and France, the following topics will stand out in our mind as we read the article
- World cup
- Soccer
- Croatia
- France
Topic modeling algorithms are essentially unsupervised machine learning algorithms, that learn these topics or concepts given a corpus of training data. It’s comparable to clustering for structured data.
With some topic modeling algorithms, a document will be represented as a probability distribution of topics. A topic will be represented as a probability distribution of words. For the example above, if the model is trained properly, we will find a topic with high probability of the words world cup, another with high probability of the word soccer and so forth.
Topic modeling algorithms are as follows. The first one is deterministic and based on matrix factorization. The other two are probabilistic.
- Latent Semantic Indexing (LSI)
- Probabilistic Latent Semantic Indexing (PLSI)
- Latent Dirichlet Allocation (LDA)
We will be using LDA for topic modeling. It’s a probabilistic generative model and is considered the best among the 3 algorithms listed.
Here are some of the NLP problems that could benefit from Topic Modeling based solution.
- Document summarization
- Document similarity
- Document clustering
Latent Dirichlet Allocation
LDA is a probabilistic generative model. In probabilistic generative model, the focus is on the distributions of a model that’s most likely to generate the observed data, which in our case in a training corpus. The underlying model has the following features
- A document is represented as random mixture over latent topics
- Each topic is represented as a distribution over words
Training the LDA model boils down to an optimization problem that is solved to find the optimum parameters for the model distributions, such that that trained model is most likely yo generate the observed corpus.
The generative process for generating all the words in all documents is as follows. The generative process involves some prior distributions
for each document
sample document length i.e number of words from a Poisson prior distribution
choose topic distribution for a document from a Dirichlet distribution
for each word in document
sample a topic from topic distribution
sample a word from word distribution conditioned on topic
The output of LDA consists of the following two distributions, one set of distributions for documents and another set for the topics
- For each document, topic distribution over the document. More skewed the distribution, fewer the number of underlying topics for the document
- For each topic, the word distribution over the topic. More skewed the distribution, more specific the topic is.
As humans, we may be able to associate a label with a topic, but an algorithm can only define a topic as distribution over words.
I am using user friendly Python wrapper class around gensim LDA implementation. All the configuration parameters algorithm related or otherwise are provided through a properties file.
Pre Processing of Corpus
I downloaded some content by doing web search on 2 topics deep learning and block chain. I didn’t collect a large corpus. So the quality of the trained model could be improved with a larger corpus. Any NLP task requires pre processing of the corpus. The pre processing steps I have used are as follows
- tokenize
- convert to lowercase
- remove stop words
- remove punctuation
- lematize
Selecting Number of Topics with Perplexity
The first issue that comes up in Topic Modeling whether with LDA or some other algorithm, is deciding the number of topics to use. Given a corpus, it’s impossible to tell how many underlying topics are there. This problem is akin selecting the number of clusters for clustering analysis of structured data.
We will use a metric called perplexity. Perplexity is a measure of how well a language model predicts the test corpus. We will perform LDA training of a corpus for varying number of topics within a range. The perplexity goes down with increasing number of topics and then plateaus. The number of topic corresponding to the the inflection point in the plot is the optimum number of topics for the given corpus.
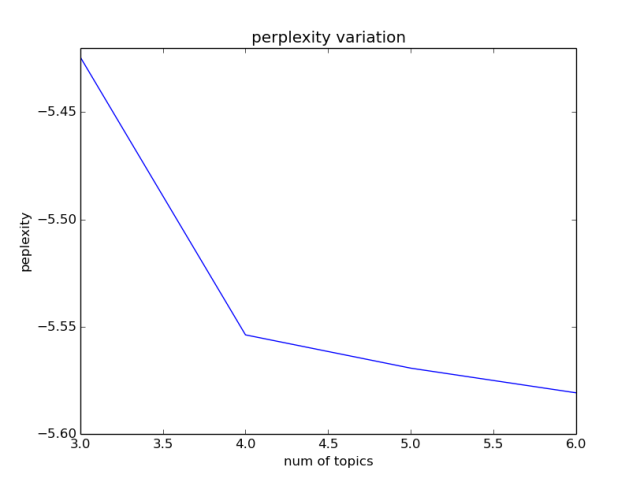
From the plot, we find an inflection point for number of topics 4. So we will use 4 topics for training the corpus. The plot is based number of topics in the range 3 to 6. Although I downloaded content for 2 topics, I knew that content downloaded based on search will not be crisp around the 2 topics only. I was expecting content to diffuse into more topics.
LDA Model Training
The model was trained with 4 topics. I have used the Python gensim library for LDA. Here is some sample output for one document.
[php]
** next doc data/topics/train/f1
doc topic distribution [(3, 0.98103637)]
filtered doc topic distribution [(3, 0.98103637)]
topic with distr : (3, 0.98103637)
filtered topic word distribution [(u’transaction’, 0.045187157), (u’cost’, 0.028959129), (u’second’, 0.021270474), (u’financial’, 0.019965205), (u’payment’, 0.017225131), (u’company’, 0.017221846), (u’said’, 0.01721893), (u’blockchains’, 0.017203245), (u’new’, 0.01647185), (u’world’, 0.01590428), (u’distributed’, 0.013179664), (u’internet’, 0.013179018), (u’computer’, 0.013178549), (u’million’, 0.013175822), (u’bank’, 0.013171356), (u’computation’, 0.013170297), (u’ledger’, 0.013167395), (u’lower’, 0.013167392), (u’per’, 0.013167375), (u’database’, 0.013167371), (u’value’, 0.013167362), (u’mufg’, 0.013167353), (u’trust’, 0.0131641105), (u’industry’, 0.013145783), (u’used’, 0.013134431), (u’even’, 0.013120084), (u’service’, 0.012166315), (u’information’, 0.009119701), (u’like’, 0.009119086), (u’application’, 0.009118958)]
final doc word distr [(u’transaction’, 0.04433024302124977), (u’cost’, 0.028409957885742188), (u’second’, 0.020867109298706055), (u’financial’, 0.01958659291267395), (u’payment’, 0.01689848117530346), (u’company’, 0.01689525693655014), (u’said’, 0.01689239777624607), (u’blockchains’, 0.016877008602023125), (u’new’, 0.016159484162926674), (u’world’, 0.015602676197886467), (u’distributed’, 0.01292972918599844), (u’internet’, 0.012929095886647701), (u’computer’, 0.012928635813295841), (u’million’, 0.012925960123538971), (u’bank’, 0.01292157918214798), (u’computation’, 0.012920540757477283), (u’ledger’, 0.012917693704366684), (u’lower’, 0.01291769091039896), (u’per’, 0.012917673215270042), (u’database’, 0.012917669489979744), (u’value’, 0.012917661108076572), (u’mufg’, 0.012917652726173401), (u’trust’, 0.012914471328258514), (u’industry’, 0.012896491214632988), (u’used’, 0.012885354459285736), (u’even’, 0.012871279381215572), (u’service’, 0.011935597285628319), (u’information’, 0.008946757763624191), (u’like’, 0.008946155197918415), (u’application’, 0.008946029469370842)]
[/php]
Dissection of the output with explanation is as follows
- doc topic distribution – Topic distribution for the document. It’s showing only 1 topic. There is minimum probability threshold, which filters out other topics from the output. The topic distribution highly skewed i.e has low entropy
- filtered doc topic distribution – Top topic distribution for the document. It’s done by probability odds ratio threshold. It picks the top n topics such that the ratio of sum of the probabilities of the top n topics to the sum of the probabilities of the remaining topics is above some defined threshold
- topic with distr – Shows the current topic. the logic loops through all the topics for a document
- filtered topic word distribution – Top n words for a topic. Top n are selected using the same probability odds ration threshold as in document topic distribution. Compared to the topic distribution, the word distribution has more spread or entropy. Looking at the words for the topic we can easily tell that that the topic is about block chain.
- final doc word distr – Word distribution for the document. This obtained by marginalizing over all the topics for a document
A close look at the words for a topic tells us that there are lot of common words. They are not necessarily related to the topic. I will address the issue later.
With LDA, when you have a new document, there are three options to analyze it. The third option should be preferred as the corpus size grow and you think you have used enough training data for building a good model.
- You can retrain the model with the new document along with the documents used so far in training the model
- You can incrementally train the model with the new document. With this option, the first option is hardly ever needed.
- Use the existing trained model to analyze the new document to get topic distribution for the new document.
Enhancing Query Result
Next we will how discuss how to leverage the topic modelling results for improving query results for Elastic Search or Solr. We will discuss two approaches, one based on enriching the documents with topic modelling results and the other based query expansion.
A document can be enriched by taking the following steps, while saving and indexing the document.
- Store topic words for a document in a separate field called topic or concept.
- Give higher boost to this field when storing and indexing the document.
If the query includes one or more topic words, the document will get a higher score because of the higher boost assigned to the topic field and will appear early in the search result. However, there is a big If. This solution will work only if the query includes the topic words.
With query expansion, the query vector is essentially altered to increase recall in the query result. This approach will require the topic words to be stored in a separate field with higher boost as in the first approach. Following steps could be taken for query expansion
- Use the original query and execute the query.
- From the query result, take top n documents.
- Take the topic words from the top n documents and add them to the original query vector.
- Execute the query with the expanded query vector and return the result
In step 3, we select the relevant document, by assuming that the top n documents are relevant. This approach is called Pseudo Relevance Feedback in Search Engine literature. Ideally, the relevant document are those documents from the initial query result , that the user has interacted with.
Filtering Out Common Words
I alluded to this problem earlier. Common words are words that are not part of the vocabulary of the topics for the domain under consideration. They are just part of general vocabulary and don’t have any discriminating power to identify a topic.
Some examples of such words from the output shown are company, world, value. How do we filter such words out from the topic word distribution. We will discuss two approaches.
The first approach is based on selecting the appropriate range of term frequency distribution. LDA being a vector space model, uses term frequency distribution of a document as the basic input. In gensim term frequencies and vocabulary is handled through a Dictionary class.
The terms that represent the underlying topic tend to be somewhere in between the frequency extremes. Frequencies of such terms are neither too high nor too low. The gensim dictionary library provides two parameters that can be used to select the appropriate frequency range.
The second approach is based on the intuition that terms that are truly representative of a topic will have a higher normalized frequency or probability in a domain specific corpus compared to a general baseline corpus.
One measure for the probability difference is Relative Entropy or Kullback Leibler divergence. For each word, we consider the probability of a word in domain specific corpus and in a general corpus. Then we calculate relative entropy.
If the relative entropy is positive, then the word is more representative of the domain under consideration, compared to words with negative relative entropy. I address this problem in more details in a future post with more details.
Summing Up
This post is about marriage of search technology with NLP. We have used topic modeling to improve query result for search engines like Elastic Search or Solr. The tutorial for building the LDA model is available.
Originally posted here.





